Good statistical design is a key aspect of meaningful research. Elements such as data robustness, randomization and blinding are widely recognized as being essential to producing valid results and reducing biased assessment. Although commonly used in in vivo animal studies and clinical trials, why is it that these practices seem to be so often overlooked in in vitro experiments?
In this thread we would like to stimulate a discussion about the importance of this issue, the various designs available for typical in vitro studies, and the need to carefully consider what is ‘n’ in cell culture experiments.
Let’s consider pseudoreplication, as it is a relatively serious error of experimental planning and analysis that hasn’t received much attention in the context of in vitro research.
The term pseudoreplication was defined by Hurlbert more than 30 years ago as “the use of inferential statistics to test for treatment effects with data from experiments where either treatments are not replicated (though samples may be) or replicates are not statistically independent” (Hurlbert SH, Ecol Monogr. 1984, 54: 187-211). In other words, the exaggeration of the statistical significance of a set of measurements because they are treated as independent observations when they are not.
Importantly, the independence of observations or samples is (in the vast majority of cases) an essential requirement on which most statistical methods rely. Analyzing pseudoreplicated observations ultimately results in erroneous confidence intervals, that are too small, and inaccurate p-values as the underlying experimental variability were underestimated and the degrees of freedom (number of independent observations) were incorrect. Thus, the statistical significance can be greatly inflated leading to a higher probability of Type I error (falsely rejecting a true null hypothesis).
To add to the confusion, the word ‘replication’ is often used in the literature to describe technical replicates or repeated measurements on the same sample unit, but can also be used to describe a true biological replicate, which is characterized as “the smallest experimental unit to which a treatment is independently applied” (link).
To understand pseudoreplication-related issues, it is therefore crucial to carefully define the term biological replicate (= data robustness) in this context and to distinguish it from a technical replicate (= pseudoreplicate): The critical difference here (as proposed by M. Clemens: link) is whether or not the follow-up test should give, in expectation, exactly the same quantitative result as the original study. A technical replication re-analyses the same underlying data set as used in the original study, whereas a biological replicate estimates parameters drawn from different samples. Following this definition, performing pseudoreplication tests does not introduce independency into the experimental system and can mainly be applied to measure errors in sample handling as the new findings should be quantitatively identical to the old results. In contrast, robustness tests represent true biological ‘replicates’ due to independent raw materials (animals, cells, etc.) used and therefore do not need to give the same results as obtained before. Only a robustness test can analyze whether a system operates correctly while its variables or conditions are exchanged.
In the following experiment, cells from a common stock are split into two culture dishes and either left untreated (control) or stimulated with a growth factor of interest. The number of cells per dish is then used as the main readout to examine the effect of the treatment. The process of data acquisition will have a decisive impact on the quality and reliability of the final result. These are different options on how to conduct this experiment:
FIRST: After a certain period of time, 3 different cover slides are prepared from each dish to calculate cell numbers, resulting in six different values (three per condition).
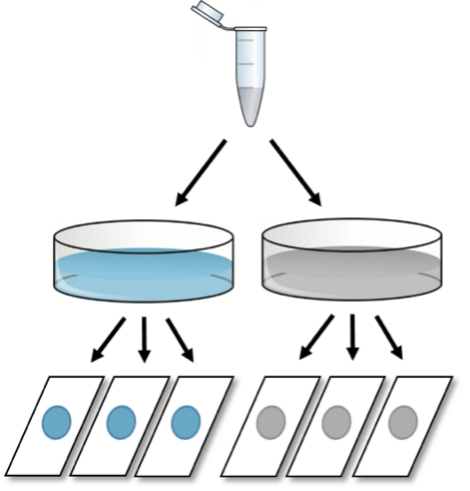
Although there were two culture dishes and six glass slides, the correct sample size here is n=1, as the variability among cell counts reflects technical errors only, and the three values for each treatment condition do not represent robustness tests (= biological replicates) but technical replicates.
SECOND: A slightly better approach is to perform the same experiment on three different days, counting the cells only once per condition each day.
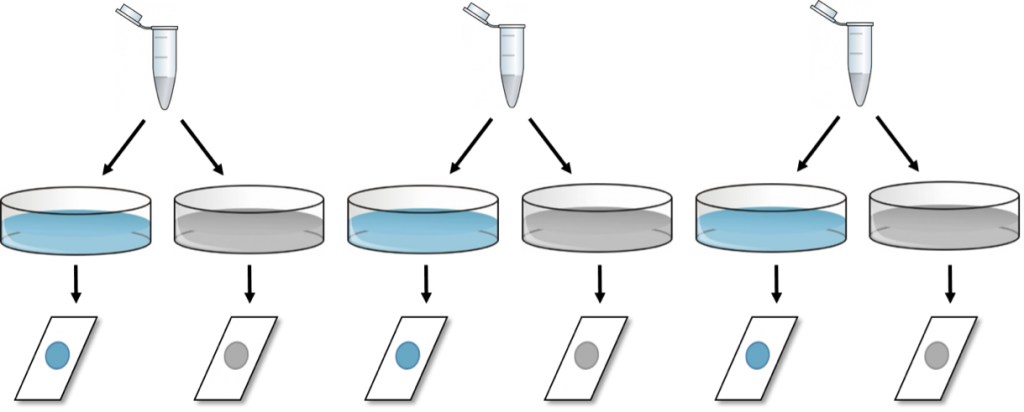
This experiment indeed shows “n” equal three.
This approach gives the same number of final values (six), yet, independency is introduced (in the form of time) due to repeating the experiment at three separate occasions, resulting in a sample size of n = 3. Here, the two glass slides from the same day should be analyzed as paired observations and a paired-samples t-test could be used for statistical evaluation.
THIRD: To further increase confidence in the obtained results, the three single experiments should be performed as independently as possible, meaning that cell culture media should be prepared freshly for each experiment, different frozen cell stocks and growth factor batches, etc. should be used.
It is reasonable to assume that most scientists who have performed in vitro cell based assays will have gotten as far as to consider and apply these precautions. But now we must ask ourselves: do those measurements actually account for real robustness tests? When working with cell-based assays, it is important to consider that, even if for each replicate a new frozen cell stock was used, ultimately all cells originated from the same starting material, therefore no biological replicates can possibly be achieved.
This problem can only be solved by generating several independent cell lines from several different human/animal tissue or blood samples, which demonstrates that reality often places constraints on what is statistically optimal.
The key questions, thus, are: ‘How feasible is it to obtain true biological replicates and to satisfy all statistical criteria?’ or ‘How much pseudoreplication is still acceptable?’
We all know that cost and time considerations, as well as the availability of biological sample material, are important; and quite frequently these factors force scientists to make compromises regarding study design and statistical analysis. Nevertheless, as many medical advances are based on preclinical basic in vitro research, it is critical to conduct, analyze and report preclinical studies in the most optimal way. As a minimum requirement, when reporting a study, the design of the experiment, the data collection and the statistical analysis should be described in sufficient detail, including a clear definition and understanding of the smallest experimental unit with respect to its independence. Scientists should also be open about the limitations of a research study and it should be possible to consider and publish a study as preliminary or exploratory (using ‘pseudo-confidence intervals’ instead of ‘true’ confidence intervals, when over-interpretation of results should be avoided) or to combine results with others to obtain more informative data sets.
As mentioned above, even if samples are easy to get or inexpensive, it can be dangerous to inflate the sample size by simply increasing the number of technical replicates, which may lead to spurious statistical significance. Ultimately, only a higher number of true biological replicates will increase the power of the analysis and result in quality research.
In this context, and to understand the extent of the problem, it would be quite informative to perform a detailed meta-analysis of articles about in vitro research studies to get an idea about the ratio of biological and technical (and unknown) replicates used for the scientific conclusion!
13 Comments
Great post.
Thank you!
Please share it, if you find it useful!
Warmest,
Björn
Thank you for sharing your ideas! There are, nevertheless, some
pitfalls in regards to clinic. Once I was a school student,
I thought how one should tackle this problem but I'd always
come across some funny responses: go google it or even ask a friend.
What if my friends don't have sufficient knowledge or expertise to assist me?
What when I googled it multiple times and couldn't locate the solution? That is when posts
like this one can provide proper advice on the issue.
Once again, thank you for the job!
The more I read, the better your content is.
I've covered a lot of those other resources; nonetheless,
just here, I've found valid information with such essential facts to keep in mind.
I suggest you'll publish articles with different topics to update our knowledge,
mine specifically. The language is just another thing-just brilliant!
I believe I've already found my perfect source of the most up-to-date info,
thanks to you!
Thank you for this post. Very interesting. Although, I still have a difficult time to wrap my head around this. For example, I have one experiment we have done in which we have three mice per group and in total 4 different groups. We are studying one tissue that has been extracted from each mouse brain. For each animal, we have three blocks of tissue and for each block, we have studied five cell bodies using electron microscopy. We have counted the number of mitochondria per cell body.
I understand that the basic assumption when using Anova is that each value represents an individual sample and that we are assuming independence between values. Thus, averaging all our counts per block would lead to n=3 per group. However, my concern is that averaging all of these technical replicates and running statistical analyses on average values means losing potentially important information. Looking at the raw data we naturally observe quite some variability, hence “my concern”. For In vitro assays, with cells that have ben cultured in a dish from one sample, I agree that this should be considered a "technical replicates". However, in our experiment, the method per se (counting) is not resulting in variance, but the "biology is" as the number of mitochondria varies greatly per cell body. A sample size of 3 or 9 or 45 of course impacts the statistical analysis (Anova). Would love to hear your opinion on this.
Dear Kristina,
Thank you for posting your question on our website. If I understand your question correctly the differentiation between technical and biological replicates is at the core of it. My answer has a theoretical and a more pragmatic component to it.
Theoretic: Common statistical tests assume that the samples in each group are independent form each other. The underlying math reflects that. Obviously, multiple samples from one animal are not independent of each other. That does not preclude analyzing them but based on applying different assumption would imply using different math to analyze the probability that the observation could have been made based on chance alone. Thus, treating technical replicates as biological replicates violates assumptions that went into the calculation of the p-value, which makes the p-value a less reliable witness.
Pragmatic: Let’s assume that one animal had something unexpected happening such as a virus infection that ultimately affects the parameter you measure. If you treat the mean/median from all cells of one animal as your biological replicate, that animal would perhaps look like an outlier (although determining whether something is an outlier is challenging based on small sample sizes such as n = 3; but that is a different issue). On the other hand, if you took each cell as replicate and have e.g., 5 per animal, the same data would no longer look like an outlier, just like a sample with a lot of variability.
Let’s play a bit more with this idea: If you treat the mean/median of all cells from an animals as your biological replicate, sample size goes down, which reduces your statistical power. On the other hand, the mean/median of all cells from an animal is a more precise estimate of the true biology in that animals, so variability goes down, which increases statistical power. Thus, the two effects offset each other to some degree. Whether your overall power goes up or down depends on specifics of a given dataset including how many technical replicates go into one biological replicate and how large the variability between technical replicates is. However, I assume that in most cases using the biological replicates will lead to a reduced power. That’s news one does not like to hear, but unfortunately that is the situation.
And there is an additional layer of complexity: let’s take an experiment as example where cells are isolated from the heart, placed into a dish and certain currents are measured by electrodes in such cells. If the cells come from healthy and diseased animals and I wish to learn whether disease affects the current, I would count all cells from one animal as technical replicates and their mean/median as biological replicates. The reason being that if I had different numbers of cells from each animal (very common in such experiments), an animal with more successfully measured cells would weigh heavier in the mean/median of biological replicates than if each animals weighs in at n = 1. On the other hand, I may wish to use the same cells to determine the properties of a drug on the gating of the channel. In that case I could see a good reason for using each cell as a biological replicates, because the outcome depends on the interaction between the compound and the channel in each cell and is not expected to exhibit major differences between underlying animals to begin with.
Bottom line: this is a complex issue. The answer depends partly on what the purpose and type of the experiment is. Leaving that aside, the analysis type you choose implicitly makes assumptions; if these assumptions are not met, the calculated p-values may be invalid. I understand that it is unpleasant news if that leads to a greater number of animals being needed, but please don’t decapitate the bearer of bad news.
I hope that this was helpful to you. Please feel free to let me know if there are follow-up questions.
Kind regards,
Martin Michel
Thank you for this important post. I use cells from a cell line to measure cell viability after treatment of 3 drugs at 5 different concentrations. I measure the cell viability only at 24 h. Of course, I have repeated the experiments several times. Are my data from the same day of experiment paired, regarding that they are from the same cell passage? There are many opinions on this issue. Others say they are not considered paired, as the same well (from 96-well plate) did not receive all the 3 treatments, and different group of cells (from the same fask) received different treatment. I would really appreciate your opinion on this.
It is very difficult to answer this very specific question. The general idea behind pairing is to eliminate variability that is introduced by major differences in the baseline values. For instance, assume that baseline values are 1, 10, 75 and 3000 and corresponding treatment values are 2, 17, 120 and 4730. It is very clear that with pairing you see a consistent increase. Most likely better expressed as fold increase than as absolute increase. On the other hand, unpaired analysis of these hypothetical data would not show a clear increase because the error bars are tremendous both at baseline and after intervention. In this case pairing clearly helps to reveal what the data tell us. Let’s take another hypothetical example: at baseline we have 15, 22, 32 and 44 and after treatment 22, 17, 33 and 48. In this case, the variability does not mainly come from that between baseline values and pairing does not help. In the best of all worlds, one would know prior to the study whether realistically a large variability between baseline is to expect and decided based on that whether to pair (and whether to look at fold or at absolute change). If such decision was not made before the experiments, the only way out is to transparently communicate the data on a scatter plot also showing the pairing (even if the data are not analyzed as paired). If the decision whether cell counts change is important (for instance if cell survival has been the main purpose of the study) and no decision was made before start of the experiments, it may be necessary to repeat the experiments. Please note, that these are general considerations, and more specific advice cannot be provided based on the information you provided.
Thank you for your post, which is very useful.
I also have a question about my experiment:
In my experiment, I have 12 rats in 3 different genotypes (Homozygous, Heterozygous, WT). For each rat in each genotype, we isolated brain tissues from 4 different brain areas (hippocampus, prefrontal cortex, cerebellum, corpus callosum). We want to perform RNA-seq to check the gene knockout's influence on the transcriptome.
I just do not know, if I want to study the influence on the whole rat brain, could I mix the results of tissues from different brain areas? For example, for rat1, there are sample 1 (hippocampus) , sample 2 (prefrontal cortex), cerebellum sample (sample 3), corpus callosum (sample 4). Could I regard them as 4 technique replicates for the same animal? Or I can not mix them for the whole brain analysis?
Dear Reader,
thank you for posting here.
If this experiment has already been conducted (i.e., tissue from all 12 rats per group collected, processed, and sequenced), then we would suggest to treat the study as exploratory, state so explicitly in the publication and present data with regions averaged / summed as well as with each region separately. Or, if such possibility exists, based on the results of this exploratory study, run another confirmatory experiment. Please also see more information on this in the EQIPD Toolbox.
If the experiment has not yet been conducted, one would need to discuss its design. In this case, please contact us.
Many thanks for your reply! I have contacted with you already!
Thank you for this very interesting post!
Let's say I'm doing an experiment with P. gingivalis W83 cells (control vs treated) and have 6 biological replicates (n=6). What sampling method (random/non-random; what specific type of random/non-random sampling method) is used in this case? Or is this question not applicable in in-vitro experiments?
Leave A Comment